The Problem
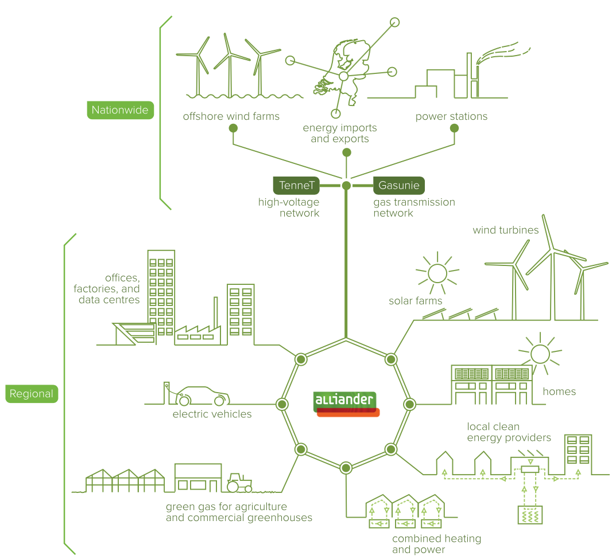
Dutch DSO Alliander is faced with the challenge of increasing the capacity of their network within the next 10 years by the same amount as within the past 100 years. On top of that, novel technologies like solar panels and electric vehicles add additional complexities to this future network. Performing large grid calculations on this future network may become classically intractable.
Together, Alliander and QAL embarked on a journey to explore the potential usefulness of quantum computing for determining whether energy grids are robust enough to sustain potential cable outages. In the DSO community, this problem is referred to as the “N-1 problem”, and it comes down to being able to reroute the energy flow through a grid for every potential single-cable outage.
The Quantum Solution
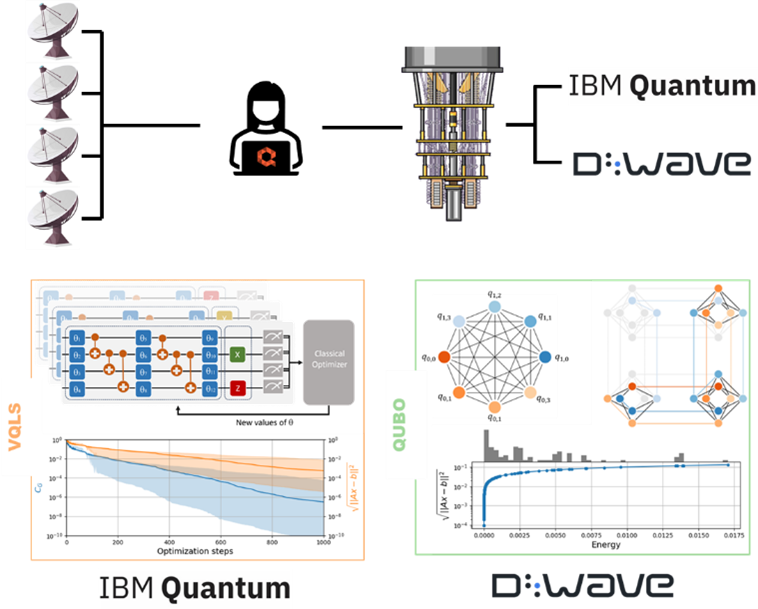
During this initial collaboration, 3 potential quantum computing solutions were researched. Aimed at more fault-tolerant usages of quantum computing, the first method was based on amplitude amplification. By preparing a superposition over many different network configurations, we exploit quantum parallelism to efficiently find a valid network reconfiguration. In the second approach, we used quantum annealing, encoding our problem as a Quadratic Unconstrained Binary Optimization problem to let a quantum system adiabatically evolve towards our preferred solution. Lastly, we explored the use of Gaussian Boson Samplers for efficiently checking connectivity of networks after a cable outage disconnects them.
The Benefits
The amplitude amplification algorithm was tested on quantum emulators and was successfully run to solve the N-1 problem for graphs of up to size 7. Quantum annealing was run on D-Wave’s advantage system to solve the N-1 problem for graphs of size 4. The potential of photonic quantum computing was explored using QuiX Quantum’s Gaussian boson samplers.
These results indicate that as hardware quality and size advance, robustness of large systems that is classically incomputable, could potentially be verified on a quantum computer.
This work is supported by the Dutch National Growth Fund (NGF), as part of the Quantum Delta NL programme